- A BCD counter is a 4-bit binary counter that counts from 0 to a predetermined count using a clock signal. When the count reaches the predetermined value, it resets all of the flip-flops and begins counting again from 0. This type of counter is built with four JK flip-flops and counts from 0 to 9, with the result represented digitally. It resets and restarts after reaching the count of 9 (1001).
- A decade counter is so named because it counts ten distinct combinations of the applied input. In binary format, a BCD counter counts 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and many other values. A four-bit decade counter acts as a BCD counter by skipping any 6 of the 24 outputs. The 74LS90, an asynchronous decade counter, is the most common implementation of this counter.
- A BCD counter built with a JK flip flop is shown below. The J and K terminal outputs are connected to logic ‘1’. Except for the last flip flop, the clock signal’s input in each flip flop is connected to the next flip flop. For all flip-flops, the NAND gate output is connected in parallel to the CLR signal.
BCD or Decade Counter Circuit
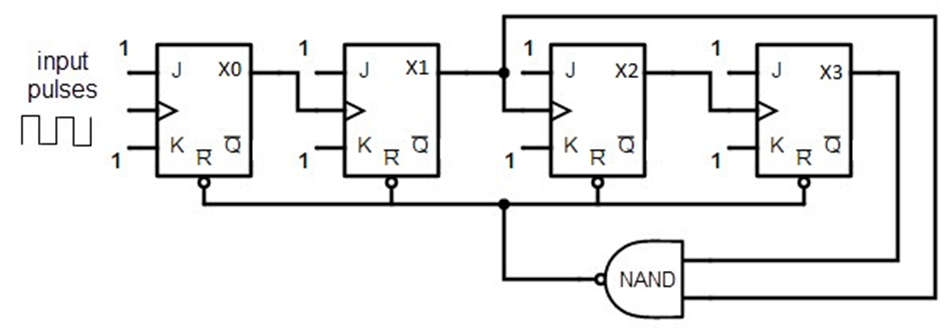
- When the decade counter is in REST mode, the count equals ‘0,’ which is 0000 in binary, and this is the beginning of the counter cycle. When a clock signal is connected to the circuit as an input, the circuit begins to count the binary digits in sequence. The initial clock pulse can count to 9 digits, or up to 1001. The count then increases to 10 with the arrival of the next clock pulse, which is 1010.
- According to the image above, ports X1 and X3 will be high. In the case of high inputs, the NAND gate’s output is at a low position. This output is then connected as an input to the CLR signal, which resets all of the flip-flop stages in the BCD counter. This means that the pulse count from 1001 will reset and begin from ‘0000’.
Truth Table and State Diagram of Decade Counter
- The decade counter’s truth table describes the counting functionality. It represents the circuit’s count in decimals for input pulses. When the circuit count is 10, the output of the NAND gate is ‘0,’ which means 1010. This count is then decoded using the NAND gate inputs X1 and X3. When the count number reaches ’10,’ the NAND gate flips from ‘1’ to ‘0,’ resetting all the flip-flops.
| Input Pulses/Clock Pulses | QD | QC | QB | QA |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0(Resets) |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
- The operation of the decade counter is explained in four stages in the circuit diagram, with each stage containing a flip flop. As a result, the circuits are capable of counting 16 states (i.e. 16 bits), but only 10 of them are used. The circuit counts from ‘0’ to ‘9,’ and then the NAND gate resets the circuits and begins counting again from ‘0,’ which is 0000. In this manner, many counters can be linked in series to count up to the required number.
- The number that the BCD circuit can count is referred to as “Modulus,” also known as “Mod”. When a counter automatically resets after counting ‘n’ bits, it is referred to as a Mod-n counter, where ‘n’ is an integer. The Mod counter has a range of ‘0’ to ‘2n – 1’. There are numerous types of counters, including Mod 4, Mod 8, Mod 5, and Mod 16 counters, among others.
74LS90 Decade Counter
- We use the IC name 74LS90 to solve this problem. The IC includes two MOD counters. The first is a MOD 2 counter, and the second is a MOD 5 counter. The counter begins counting from 0000 to 1001, then resets the value. The automatic reset causes the counter to begin at 0 and end at 9. We have four reset pins on the IC that we can use to enable the counter by activating specific two pins. The IC is TTL-based and thus compatible with other TTL-based counters and ICs.
- The operation of the 7490 will be explained in this section. The internal structure of the IC consists of four flip-flops, the first of which serves as MOD 2 and the other three as MOD 5. The output state will be changed by using the two clock pins. The reset pins are controlled by an AND gate.
- The IC has four reset pins, two clock pins, and four output pins. Before we can use the IC, we must first understand the reset pins. The output will be controlled by these four reset pins. These four reset pins will generate multiple 16 combinations, but some of them will produce fixed output. The table is shown below.
| MR1 (R4) | MR2 (R2) | MS1 (R2) | MS1 (R1) | QD | QC | QB | QA |
|---|---|---|---|---|---|---|---|
| H | H | L | X | L | L | L | L |
| H | H | X | L | L | L | L | L |
| X | X | H | H | H | L | L | H |
| L | X | L | X | COUNT | – | – | – |
| X | L | X | L | COUNT | – | – | – |
| L | X | X | L | COUNT | – | – | – |
| X | L | L | X | COUNT | – | – | – |
- To keep MOD 2 and MOD 5 in sequence, connect the second clock pin (Pin 1) to the LSB of the IC. The clock input signal to the IC will be provided by the first clock pin (Pin 14). The output will be affected as the state changes from HIGH to LOW. However, keep in mind the concept of the reset pins; otherwise, the IC will output some random value or no output. The complete functional circuit is shown here. When we give the pulse, the IC will output the result in binary form. Every binary form corresponds to a decimal number.
Applications of BCD Counter Circuit
- Clock circuits.
- Frequency dividers.
- Frequency counting circuits.
- State machines.
- Sequencers.
- Clock division.
- CMOS low power circuits.
- Integrated oscillators.
- Clock generation.
- Used as inputs compatible with TTL etc.